Projektbeschreibungen

1. Kryptoanalyse – FITRFXUYYIYPRWVR?
2. Bilderkennung mit Künstlichen Neuronalen Netzen
3. Augmented Reality auf iOS-Geräten
4. Optimierungsalgorithmen in Graphen mit Python
5. Der Symmetrie auf der Spur
6. Spielen mit Struktur – Gesellschaftsspiele und Mathematik?!
7. Grundpfeiler der Mathematik
8. Smartify your Life
9. Unterwegs auf Datenexploration - Wie geht es unserer Umwelt?
10. Quantencomputer
11. „Matrix revolutions“ – Von Abbildungsmatrizen bis zur Hauptachsentransformation
12. Gamecontroller entwickeln und konstruieren
13. Spieleprogrammierung wie ein Profi!
14. Die Mathematik der Sudokus
15. Ein Streifzug durch die komplexen Zahlen
16. Symmetrien – Eine visuelle Darstellung von Fries- und Kristallgruppen
17. Autonomes Fahren in der Simulation mit Python und Godot
18. Ein Weg unter vielen - Dreidimensionale Simulation eines Labyrinths

1. Kryptoanalyse – FITRFXUYYIYPRWVR?

Mirko Igel

Wenn ja, dann bist Du hier genau richtig. In diesem Projekt geht es nämlich darum, Codes zu knacken. Natürlich wird es dazu notwendig sein, sich mit den verschiedenen Verschlüsselungsmethoden vertraut zu machen. Dabei geht es natürlich vorrangig um solche Verfahren, die mit Zettel und Stift ausgeführt werden können, diese finden übrigens selbst im Zeitalter des Computers durchaus noch Anwendung.

Aus diesem Bereich der potentiell knackbaren Verfahren existieren einige äußerst interessante und bis heute ungelöste Rätsel. Beispielsweise die Hinweise des Zodiac-Killers (eines Serienmörders, der in den 60er und 70er Jahren sein Unwesen in Kalifornien trieb), die (bis heute?!) nicht entschlüsselt werden konnten.

Das Themengebiet bietet also durchaus das Potential, um berühmt zu werden.

Voraussetzungen

Spaß am Knacken von Rätseln und an Mathematik. Auch wenn keine Vorbildung aus der Informatik notwendig ist, wäre es schön, wenn sich auch solche Teilnehmer finden würden, die (ein wenig) Programmieren können – die Programmiersprache ist dabei beliebig. Denn dann ließen sich ggf. Werkzeuge entwickeln, die das Code-Knacken vereinfachen können.

2. Bilderkennung mit Künstlichen Neuronalen Netzen

Christian Spallek

In den letzten Jahren hat es im Bereich der Künstlichen Intelligenz gewaltige Fortschritte gegeben. Von zentraler Bedeutung ist dabei die Entwicklung immer komplexerer Künstlicher Neuronaler Netze (KNN), die zu Durchbrüchen auf den Gebieten der selbstfahrenden Autos, Bild- und Mustererkennung, Sprachverarbeitung sowie Text- und Bildgenerierung führte.

In unserem Workshop wollen wir ein wenig hinter die Kulissen der KNN schauen. Dazu werden wir zunächst deren mathematische Grundlagen erarbeiten und dann ein sogenanntes Multi-Layer-Perceptron von Grund auf selbst entwerfen, in Python programmieren und anschließend trainieren, um Bilddateien zu klassifizieren. Auf den Einsatz von KI-Bibliotheken wie Keras oder Tensorflow wird dabei bewusst verzichtet.

Voraussetzungen

Grundlagenkenntnisse in einer objektorientierten Programmiersprache sind empfohlen. Die notwendigen Sprachkonzepte in Python werden im Workshop vermittelt.

3. Augmented Reality auf iOS-Geräten

Udo Hilwerling & Dennis Gehlen

Unter Augmented Reality („erweiterte Realität“) versteht man die Verbindung computergenerierter Grafikelemente mit Kamerabildern in Echtzeit. Apple iOS ist die größte Augmented-Reality-Plattform der Welt. In diesem Workshop werden wir lernen, wie die iOS-Bibliothek ARKit Eckpunkte der realen Umgebung erkennt, dem Grafiksystem zuführt, die Koordinatensysteme anpasst, Bewegungen erfasst und vieles mehr. Auch das Erlernen der java-ähnlichen Programmiersprache Swift, die von Apple benutzt wird, ist Gegenstand des Kurses. Am Ende der Woche wollen wir eine App präsentieren können, die von ARKit Gebrauch macht und einige der Möglichkeiten demonstriert (z. B. einen Spielklassiker „auf dem Schreibtisch“ als AR-Anwendung).

Voraussetzungen

Voraussetzung zur Teilnahme sind sichere, fortgeschrittene Kenntnisse in Objektorientierung und Java und grundlegende Kenntnisse in Englisch. Die wichtigsten Voraussetzungen sind allerdings Spaß am Programmieren und die Fähigkeit, sich in ein Projekt einzuarbeiten und -unter Hilfestellungen- selbstständig weiterzuführen; Erfahrungen im projektorientierten, kooperativen Arbeiten sind dabei von Vorteil.

4. Optimierungsalgorithmen in Graphen mit Python

Klaus Bovermann

Die Graphentheorie spielt in vielen Bereichen des täglichen Lebens eine bedeutende Rolle. Graphen werden verwendet, um bei der Lösung vieler praktischer Probleme zu helfen. Angefangen beim Königsberger Brückenproblem sind hier nur einige Beispiele genannt:

• Routenplanung mit dem Dijkstra-Algorithmus, um den kürzesten Weg zwischen zwei Punkten in einem Straßennetzwerk zu finden.
• Optimierung von Netzwerken mit dem Kruskal-Algorithmus, um optimale Spannbäume zu finden.
• Das TSP (Traveling Salesman Problem) besteht darin, eine kürzeste Rundreise durch alle Knoten eines Graphen zu finden.

In dem Workshop werden diese (und ggf. weitere) Algorithmen erforscht und in der Programmiersprache Python implementiert, so dass am Ende benutzbare Anwendungen entstehen.

Voraussetzungen

Grundlegende Programmierkenntnisse (in einer beliebigen Programmiersprache) werden empfohlen.

5. Der Symmetrie auf der Spur

Dr. Max Hoffmann

Symmetrie? Da ist doch in Klasse 6 eigentlich alles zu gesagt, oder? Mitnichten! Im Workshop werden wir uns in einer Weise mit dem Thema Symmetrie auseinandersetzen, die es uns erlaubt Inhalte der Unterstufe mit Hochschulmathematik zu verknüpfen, die auch in aktueller mathematischer Forschung relevant ist. Dazu werden wir uns zunächst damit beschäftigen, was Symmetrien aus mathematischer Perspektive sind und wie man mit ihnen rechnen kann. (Genau: "Rechnen", wie in der Grundschule, nur cooler). Darauf aufbauend werden wir mathematisch klassifizieren, auf wie viele Arten man eigentlich eine Dekorleiste im Badezimmer gestalten kann und wie viele Möglichkeiten es gibt einen Fußboden zu fliesen. Im Projekt werden wir sowohl mathematisch als auch kreativ arbeiten und komplexe symmetrische Figuren konstruieren - auch mit Hilfe von selbstprogrammierten Computertools. Eine spannende Randnotiz: Das alles funktioniert nahezu ausschließlich mit ganzen Zahlen, Brüche sucht ihr in diesem Projekt vergeblich.

Voraussetzungen

Spaß an Mathematik und am Knobeln sowie grundlegende Kenntnisse im Programmieren. Der erste Teil des Projektes ist eher mathematisch, im zweiten Teil kann je nach Euren Wünschen mehr oder weniger stark programmiert werden.

6. Spielen mit Struktur – Gesellschaftsspiele und Mathematik?!

Marceau Speczyk & Manuel Marcel Wieneke

Gesellschaftsspiele und Mathematik?!

Dieses Projekt dreht sich um mathematische Strukturen hinter beliebten Gesellschaftsspielen, die auf den ersten Blick nichts mit Mathematik zu tun haben. So werden wir spielend Spielprinzipien analysieren, Spielstrategien entwickeln und verschiedene mathematische Konzepte und Strukturen kennenlernen, die Ideen der Schulmathematik mit typischen Inhalten des Mathematikstudiums verknüpfen. Dabei beginnen uns sogar Fragestellungen die bis heute ungelöste mathematische Probleme darstellen. Brüche oder Integrale sucht ihr hierbei vergeblich, das alles funktioniert nahezu ausschließlich mit ganzen Zahlen!

Ziel des Projekts ist es, ein eigenes mathematisches Gesellschaftsspiel zu entwerfen und am Ende der Akademie zusammen zu spielen. Voraussetzung für die Teilnahme am Projekt sind Spaß am Knobeln, Ausprobieren und natürlich am Spielen von Gesellschaftsspielen.

Voraussetzungen

keine (Kenntnisse in Tabellenkalkulationsprogrammen und Programmierung werden begrüßt, sind jedoch nicht notwendig)

7. Grundpfeiler der Mathematik

Morris Kopelke

Die Mathematik beschränkt sich nicht nur auf stumpfes Auswendiglernen und das Anwenden von Schema F. In diesem Projekt wirst du entdecken, dass Mathematik weit über diese Vorstellung hinausgeht. Wir werden uns zunächst einige Grundkonzepte und Bausteine der heutigen Mathematik genauer ansehen, um zu erkunden, welche Vielfalt und Anwendungsmöglichkeiten dieses faszinierende Fachgebiet bietet.

Wenn die Wettervorhersage für morgen eine Regenwahrscheinlichkeit von 50 % voraussagt, heißt das dann, dass es nur an 12 von 24 Stunden regnet? Oder nur auf halb Deutschland? Und was ist eigentlich das Gegenteil des Satzes: „Wenn es regnet, ist die Straße nass“? Natürlich gibt es mehr gerade Zahlen unter 1000 als Quadratzahlen unter 1000, das stimmt auch für jede andere (beliebig große) Zahl anstelle der 1000. Heißt das jetzt auch, dass es auch insgesamt mehr gerade Zahlen als Quadratzahlen gibt? Ist ein 1 x 1 großes Quadrat wirklich größer als eine 1 lange Strecke? Ergibt die Frage überhaupt Sinn? Wie können wir mehrere Objekte zu einer Gruppe zusammenfassen? Wie sieht es aus, wenn wir die Reihenfolge (nicht) beachten wollen?  kennen wir als Symbol für den Vektor von A nach B, aber was genau ist das? Der eingezeichnete Pfeil im Koordinatensystem oder doch etwas ganz anderes? Darf oder kann man wirklich nicht durch 0 teilen? Ist denn zumindest 0:0 in einer sinnvollen Weise möglich?

Im zweiten Teil werden wir einige Beweismethoden zur Lösung von Kombinatorikproblemen kennenlernen. Viele Zählfragestellungen lassen sich lösen, indem man die Situation aus 2 verschiedenen Blickwinkeln betrachtet. Manchmal reicht es auch aus, die Frage auf das Wesentliche zu reduzieren und in einen anderen Kontext zu bringen, also eine passende Sichtweise zu wählen. Die mathematische Induktion ist ein weiteres mächtiges Problemlösewerkzeug, auch die Wohlordnung der natürlichen Zahlen werden wir nutzen.

Voraussetzungen

Im ersten Teil leitet uns ein aufgeweckter Geist und das Interesse, den Dingen wirklich mal auf den Grund zu gehen. Im zweiten Teil hilft mathematische Vorerfahrung natürlich, ist aber keine Voraussetzung.

8. Smartify your Life

Daniel Spittank

In unserem Alltag haben wir es mit sehr vielen Informatiksystemen zu tun. Die beständige Zunahme der Verfügbarkeit „smarter“ Geräte durchzieht viele Bereiche der Gesellschaft, vom allgegenwärtigen Smartphone über Smartwatches und Health- und Fitnesstracker bis hin zum Smarthome.

All diese Geräte bieten uns Komfort und nützliche Funktionen, bringen aber auch ihre ganz eigenen Probleme mit sich. Viele der Geräte gleichen Blackboxen, die z.T. mit sensiblen persönlichen Daten operieren. Dies wirft gesellschaftliche Fragen auf, die mit einem informatischen Blick hinter die Kulissen geklärt werden sollen.

Aufgrund der breiten Verfügbarkeit günstiger Komponenten und Mikrocontroller bietet sich der Bereich der Smarthomes besonders an. In diesem Projekt kann es daher um die Analyse von Protokollen der Komponenten, das Reverse-Engineering von Komponenten, die Entwicklung eigener Sensoren und Aktoren, sowie die Vernetzung und Automatisierung verschiedener smarter Geräte zu einem Gesamtsystem gehen.

Voraussetzungen

Programmierkenntnisse sind hilfreich, aber nicht unbedingt erforderlich.

9. Unterwegs auf Datenexploration - Wie geht es unserer Umwelt?

Sven Hüsing & Jacqueline Anthes

In vielen Bereichen des alltäglichen Lebens spielt das Erheben und Analysieren von großen Datenmengen eine wichtige Rolle. Seien es gesellschaftliche und politische Diskussionen wie die Einführung von 30er-Zonen im Innenstadtverkehr oder persönliche Interessen wie die Reduzierung des CO2-Gehalts im eigenen (Klassen-)Raum – besonders in Bezug auf die Umwelt werden häufig Auswertungen großer Datenmengen herangezogen, wobei selbst erhobene Daten und passende Datenauswertungen dabei helfen, neue Erkenntnisse über die Umwelt zu gewinnen, darauf aufbauende Handlungsempfehlungen zu finden und damit die Umwelt und das eigene Leben zu verbessern.

Das Tolle ist: Während es früher noch schwierig war, an Umweltdaten zu gelangen, sind heute eine Menge an verschiedensten Umweltdaten für die Öffentlichkeit zugänglich und ebenfalls gibt es mächtige und gleichzeitig einfach zu nutzende (Programmier-)Tools, mit denen man die großen Datenmengen auf einem „normalen Laptop“ auswerten kann.

In diesem Projekt werden wir eigene, persönlich oder gesellschaftlich relevante umweltbezogene Forschungsfragen entwickeln, zu denen wir dann durch die Programmierung von Datenauswertungen Antworten finden und damit unsere Umwelt genauer unter die Lupe nehmen. Dafür können wir mithilfe eigens programmierter Messsensoren selbst Daten aufnehmen und zusätzlich auf Satellitendaten und sowie weitere Umweltdaten zugreifen.

Unsere gesammelten Daten werden wir dann auslesen, analysieren und visualisieren. Die Auswertung soll mit der Programmiersprache Python umgesetzt werden (Keine Sorge, wenn Ihr noch nicht in Python programmiert habt – wir werden in den ersten Tagen einen Python-Crashkurs für die Datenexploration durchlaufen J). Aufbauend darauf wollen wir Schlussfolgerungen über unsere eigene Umwelt ziehen und konkrete Handlungsempfehlungen formulieren.

Welches Erkenntnisinteresse unsere Datenanalyse lenken soll, erarbeiten wir uns in den ersten Tagen des Projektes. Eurer Kreativität sind dabei keine Grenzen gesetzt. Gerne könnt Ihr auch bereits vorher erste Gedanken und Ideen sammeln.

Voraussetzungen

Das Projekt richtet sich an alle, die Freude an Informatik und Mathematik haben. Programmiervorkenntnisse und Kenntnisse in Statistik sind nützlich, aber nicht zwingend erforderlich. Ihr solltet Euch auf jeden Fall darauf freuen (und einlassen), Programmieren als ein Erkenntnismittel (neu) kennenzulernen.

10. Quantencomputer

Dr. Hannes Stoppel

Quantencomputer sind seit einiger Zeit im Gespräch. Oft heißt es „wenn es sie gibt, ist nichts mehr sicher“. In diesem Kurs geht es darum, Grundgedanken von Quantencomputern zu verstehen. Wir werden die Struktur und der Arbeitsweise von Quantencomputern betrachten. Ein bedeutender Teil des Kurses wird auf der mathematischen Seite wie Aussagelogik und Algorithmen liegen. Die Inhalte werden wir nach Möglichkeit praktisch an einem Quantencomputer umsetzen. Dabei greifen wir nicht zuletzt auf GeoGebra, Jupyter Notebook und Qiskit zurück.

Voraussetzungen

Vorkenntnisse im Programmieren, der Informatik und der Physik sind zur Teilnahme am Kurs nicht nötig.

11. „Matrix revolutions“ – Von Abbildungsmatrizen bis zur Hauptachsentransformation

Stefanie Kessler

Den Begriff der Matrix kennst du bislang nur aus der Science-Fiction-Reihe oder aus dem Biologieunterricht? Dann wird es Zeit, die vielfältigen Anwendungen von Matrizen in der Mathematik zu erkunden!

In diesem Projekt schauen wir uns Matrizen zur Beschreibung von Abbildungen im Zwei- und Dreidimensionalen, zur Beschreibung von Prozessen und Berechnung von Wahrscheinlichkeiten, zum Lösen linearer Gleichungssysteme bis hin zu Anwendungen in der Computertomographie an. Einen Blick ins Studium kannst du werfen, wenn du dich für den Simplex-Algorithmus bei Optimierungsproblemen (Wie wird mein Erlös am größten?), für die Hauptachsentransformation (Wie verändere ich das Koordinatensystem, um ein Objekt besser zu erkennen?) und den Satz von Cayley-Hamilton (Wie können Matrizen Nullstellen einer Gleichung sein?) interessierst. Außerdem lernen wir noch ein bisschen „Handwerkszeug“ aus der Algebra und führen kleine Beweise durch. Wer mag, kann einige Inhalte in GeoGebra umsetzen.

Du rechnest gerne per Hand? Du willst wissen, wozu man die Mathematik praktisch nutzt? Dir kribbelt es in den Fingern, wenn du Zusammenhänge entdecken und beweisen sollst? Du veranschaulichst dir gerne mathematische Operationen? Dann bist du hier richtig! Das Projekt ist modular aufgebaut, sodass jede*r individuell bzw. in kleinen Gruppen Schwerpunkte aussuchen und bearbeiten kann.

Voraussetzungen

Es sind keine besonderen Vorkenntnisse außerhalb der Schulmathematik nötig. Ein solides Grundwissen in der analytischen Geometrie ist hilfreich, ebenso ein sicherer Umgang im Rechnen mit Variablen und Gleichungen. Du solltest Interesse daran haben, dir neue mathematische Zusammenhänge eigenständig oder in Gruppen zu erarbeiten. Falls du ein CAS oder ein MMS verwendest, kannst du es gerne mitbringen.

12. Gamecontroller entwickeln und konstruieren

Michel May & Oliver Girnth

In diesem Projekt bauen wir eine Spielkonsole. Wir funktionieren dafür den Arduino zu einem Gamecontroller um, indem wir Taster, Joysticks und LEDs an den Microcontroller anschließen werden. Am Computer wird dann die Spielkonsole inklusive Menü, mehrerer Spiele sowie Highscores programmiert. Sowohl der Gamecontroller als auch die Software werden individuell gestaltet, sodass eine einzigartige Spielkonsole entsteht.

Voraussetzungen

Grundlegende Programmierkenntnisse in Java sind Voraussetzung. Die Spielkonsolen können mit Programmierkenntnissen aus dem Schulstoff der Jahrgangsstufe EF entwickelt werden. Weiterführende Inhalte wie die Einbindung einer Datenbank sind möglich.

13. Spieleprogrammierung wie ein Profi!

Niklas Langkau

In dieser Projektgruppe lernen wir die Spiel-Engine Unity kennen. Unity ist eine Laufzeit- und Entwicklungsumgebung für 2D- und 3D-Spiele und interaktiver 3D-Grafik-Anwendungen. In diesem Projekt programmieren wir in Kleingruppen gemeinsam ein 3D-Jump ’n’ Run-Spiel mit dem Setting eurer Wahl.

Voraussetzungen

Kenntnisse in objektorientierter Programmierung werden vorausgesetzt (es wird die Programmiersprache C# verwendet, Kenntnisse in Java sind hilfreich).

14. Die Mathematik der Sudokus

Dr. Sara Terveer

Sudokus gehören zu den beliebtesten Logikrätseln - nicht selten sieht man Leute in öffentlichen Verkehrsmitteln oder Cafés, die Sudokus in allerlei Varianten in Zeitungen oder Apps lösen. Die Faszination ist durch das kurze und einfache Regelwerk zu erklären:

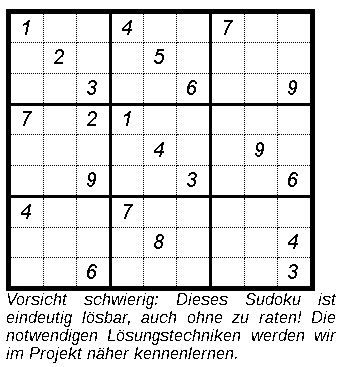
In diesem Projekt werden wir Begrifflichkeiten und Lösungstechniken aus der Welt der Sudokus kennenlernen, mathematisch formalisieren und beweisen und versuchen, einen Ansatz zur Beantwortung der obigen Fragen zu finden. Dabei werden wir einen kleinen Einblick in verschiedene Teilgebiete der Mathematik erlangen, wie beispielsweise Graphentheorie, Gruppentheorie, Kombinatorik und Logik. Und natürlich werden wir die gelernten Lösungstechniken anhand von einigen Sudokus ausprobieren!

Voraussetzungen

Freude am Rätseln und an der Mathematik. Es sind keine besonderen Vorkenntnisse über Logikrätsel, Mathematik oder Informatik erforderlich.

Bemerkung: Es handelt sich bei diesem Projekt vorrangig um ein mathematiknahes Projekt. Je nach Ermessen, Vorkenntnissen und Interessen der Projektgruppe kann im Rahmen des Projektes ein Sudoku-Solver basierend auf den erlernten Techniken entwickelt werden.

15. Ein Streifzug durch die komplexen Zahlen

Tony Prange

In diesem Projekt tauchst du in die faszinierende Welt der komplexen Zahlen ein. Dafür verlassen wir den vertrauten Raum der reellen Zahlen und stürzen uns auf die neuen Möglichkeiten, welche die komplexen Zahlen uns eröffnen. Zunächst erarbeiten wir gemeinsam die Grundlagen der komplexen Zahlen. Danach bist du gefragt: Alleine oder im Team suchst du dir aus einer Vielzahl kleiner Projekte aus, was dich am meisten interessiert. Dabei erarbeitest du dir beispielsweise, wie du mit komplexen Zahlen rechnest, wie du Gleichungen im neuen Zahlenraum löst, wie du Gleichungen – linear, quadratisch, kubisch – löst, wie du Wurzeln ziehst, wie Funktionen im Komplexen funktionieren, was Fraktale mit komplexen Zahlen zu tun haben und, und, und. Mit GeoGebra kannst du viel davon auch anschaulich visualisieren!

Voraussetzungen

Das Beste: Du brauchst keine speziellen Vorkenntnisse – nur Stift, Papier, Neugier, etwas Ausdauer und vor allem: Spaß an Mathematik!

16. Symmetrien – Eine visuelle Darstellung von Fries- und Kristallgruppen

Tanja Hommen

Dieses Projekt widmet sich der faszinierenden Welt der Symmetrien mit einem besonderen Fokus auf Fries- und Kristallgruppen. Diese Symmetriegruppen spielen eine bedeutende Rolle in verschiedenen Bereichen wie Kunst, Architektur und Natur. Ziel des Projekts ist es, eine visuelle Darstellung dieser mathematischen Strukturen zu entwickeln, indem geeignete Programmierlösungen erarbeitet werden.

Im Rahmen des Projekts werden grundlegende mathematische Konzepte der Symmetrien behandelt und in praktische Anwendungen überführt. Die Teilnehmenden erhalten die Möglichkeit, sich mit der Erstellung und Implementierung von Algorithmen auseinanderzusetzen, die zur Visualisierung dieser Muster beitragen. Dabei steht nicht nur die theoretische Auseinandersetzung im Vordergrund, sondern vor allem die praktische Umsetzung durch Programmierung.

Voraussetzungen

Für die Teilnahme am Projekt sind grundlegende Programmierkenntnisse hilfreich, jedoch nicht zwingend erforderlich. Viel wichtiger ist die Bereitschaft, sich in neue Themen einzuarbeiten und Freude daran zu haben, Probleme zu lösen und kreative Ansätze zu entwickeln. Ein gutes räumliches Vorstellungsvermögen kann dabei von Vorteil sein, um die mathematischen Konzepte besser zu verstehen und visuell umzusetzen.

17. Autonomes Fahren in der Simulation mit Python und Godot

Sören Sparmann

Autonomes Fahren gehört zu den spannendsten technologischen Entwicklungen unserer Zeit. Es verspricht nicht nur mehr Komfort und Effizienz im Straßenverkehr, sondern könnte auch die Sicherheit erheblich verbessern und langfristig den Verkehr revolutionieren. Doch hinter dieser Vision steckt eine Vielzahl technischer und ethischer Herausforderungen: Wie erkennen Fahrzeuge ihre Umgebung? Wie treffen sie Entscheidungen in komplexen Situationen? Und welche Verantwortung tragen Entwickler:innen für ihr Verhalten?

In diesem Projekt verwenden wir die Godot Game Engine, um eine Umgebung für autonomes Fahren zu simulieren. Das virtuelle Fahrzeug wird mit verschiedenen Sensoren ausgestattet. Ziel ist es, die gesammelten Sensordaten auszuwerten und darauf basierend autonome Entscheidungen zu treffen.

Das Fahrzeug verfügt beispielsweise über eine Frontkamera zur Erkennung von Verkehrszeichen und Fahrbahnmarkierungen, ein LiDAR-System zur Kollisionsvermeidung sowie GPS- und Radsensoren zur Positionsbestimmung und Geschwindigkeitserfassung. Die Sensordaten werden über eine API an ein Python-Backend gesendet, wo Algorithmen die Steuerung des Fahrzeugs übernehmen. Die simulierte Welt kann beliebig erweitert werden, um verschiedene Szenarien des autonomen Fahrens zu erproben und die KI immer weiter zu verbessern.

Neben der technischen Umsetzung stehen auch ethische Fragen im Mittelpunkt. Wie sollte ein autonomes Fahrzeug in kritischen Situationen reagieren? Wer trägt die Verantwortung, wenn es zu Unfällen kommt? Und welche Grenzen hat der Einsatz von KI im Straßenverkehr? Diese und weitere Fragen werden gemeinsam diskutiert, um ein tieferes Verständnis für die Herausforderungen und Potenziale autonomer Systeme zu entwickeln.

Voraussetzungen

Grundkenntnisse in Python sind hilfreich, aber nicht zwingend erforderlich.

18. Ein Weg unter vielen - Dreidimensionale Simulation eines Labyrinths

Volker Quade & Arzu Kocyigit

Bei einem Labyrinth, genauer gesagt einem Irrgarten, handelt es sich um ein Netz von Wegen mit Abzweigungen, Kreuzungen, Sackgassen und Wegeschleifen, die es schwierig machen, sich zurecht zu finden oder das Netz von Wegen zu verlassen. Labyrinthe kommen in der Gartengestaltung, in Palästen und Gräbern der Mythologie oder letztlich auch Computerspielen vor.

Aus Sicht des Informatikers besteht die Herausforderung nicht nur darin, einen Weg zu finden, sondern auch darin, das Wegsystem automatisiert zu erstellen.

Ziel des Projektes soll es sein, eine möglichst realistische Simulation eines Labyrinths zu entwickeln und sich darin mit algorithmischer Unterstützung zielsicher zu bewegen. Dazu gehört auch eine anspruchsvolle graphische Umsetzung mit einer perspektivischen, dreidimensionalen Darstellung, einer ansprechenden Gestaltung der Umgebung und einer wirklichkeitsgetreuen Behandlung der Lichtverhältnisse.

Um diesen Anforderungen gerecht zu werden, wird die auf OpenGL basierenden Bibliothek GLOOP verwendet. Als Programmiersprache wird Java zum Einsatz kommen.

Voraussetzungen

Die Grundlagen der objektorientierten Modellierung und Programmierung in Java sollte sicher beherrscht werden. Solide mathematische Kenntnisse und ein gutes räumliches Vorstellungsvermögen sind von Vorteil. Vorkenntnisse in der Grafikprogrammierung sind nicht erforderlich.